Pembahasan Soal UN Matematika SMA IPA 2017 No. 21 - 30_Hallo, Sobat Pejuang UN. Kali ini saya akan membahas Soal UN Matematika SMA IPA tahun 2017 part 3. Pada edisi kali ini soal-soalnya berisikan materi tentang :
- Aplikasi Turunan (Gradien Garis Singgung)
- Aplikasi Turunan (Nilai Maksimum)
- Integral Metode Substitusi
- Integral Tentu
- Aturan Sinus dan Cosinus Trigonometri
- Persamaan Trigonometri
- Mencari Nilai Jumlah dan Selisih Dua Sudut Trigonometri
- Mencari Nilai Jumlah dan Selisih pada Sinus dan Cosinus
- Sudut Antara Garis dan Bidang Dalam Dimensi Tiga
- Jarak Antara Titik, Garis, dan Bidang Dalam Dimensi Tiga.
Nah, bagi sobat pejuang UN yang ingin mengetahui pembahasan selanjutnya silahkan sobat klik pada tautan di bawah ini :
1. Pembahasan Soal UN Matematika SMA IPA 2017 Part.1 No. 1 - 10
2. Pembahasan Soal UN Matematika SMA IPA 2017 Part.2 No. 11 - 20
3. Pembahasan Soal UN Matematika SMA IPA 2017 Part.3 No. 21-30
4. Pembahasan Soal UN Matematika SMA IPA 2017 Part.4 No. 31-40
Soal Nomor 21
Diketahui grafik fungsi $y = 2x^{2} − 3x + 7$ berpotongan dengan garis $y = 4x + 1$. Salah satu persamaan garis singgung yang melalui titik potong kurva dan garis tersebut adalah .........A. $y=5x+7$
B. $y=5x-1$
C. $y=x+5$
D. $y=3x-7$
E. $y=3x+5$
Pembahasan Soal Nomor 21
BUKA
Penyelesaian :
Mencari Titik potong Grafik fungsi kurva dengan garis
$\begin{align} y_{\text{kurva}} & = y_{\text{garis}} \\ 2x^{2} − 3x + 7 & = 4x + 1 \\ 2x^{2} − 7x + 6 & = 0 \\ \left(2x-3\right)\left(x-2\right) & = 0 \end {align} \\ x_{1} = \dfrac {3}{2} \quad \text{atau} \quad x_{2} = 2 $
Selanjutnya, nilai absis $x_{1}$ dan $x_{1}$, kita substitusikan ke ke fungsi kurva atau garis untuk mendapatkan nilai ordinatnya. Agar lebih mudah kita pilih substitusikan ke fungsi garis saja.
$y = 4x + 1$
$x_{1} = \dfrac {3}{2} \; \Longrightarrow y = 4\left(\dfrac {3}{2}\right) + 1 = 7 \\ x_{2} = 2 \; \Longrightarrow y = 4\left(2\right) + 1 = 9$
Sehingga, diperoleh titik potong kurva dan garis tersebut adalah:
$\left(\frac {3}{2}, 7\right)$ dan $\left(2,9\right)$
Selanjutnya kita tentukan gradien garis singgung. Gradien merupakan turunan dari fungsi kurva $y = 2x^{2} − 3x + 7$
$m = y^{1} = \frac{dy}{dx} \\ m = 4x - 3$
Gradien garis singgung titik $\left(\frac {3}{2}, 7\right)$ adalah
$x_{1} = \dfrac {3}{2} \; \Longrightarrow m_{1} = 4\left(\dfrac {3}{2}\right) - 3 = 3$
Gradien garis singgung titik $\left(2, 9\right)$ adalah
$x_{2} = 2 \; \Longrightarrow m_{2} = 4\left(2\right) - 3 = 5$
Persamaan garis singgung titik $\left(\frac {3}{2}, 7\right)$ adalah
$\begin{align} y - y_{1} & = m_{1} \left(x - x_{1}\right) \\ y - 7 & = 3 \left(x - \dfrac {3}{2}\right) \\ y - 7 & = 3x - \dfrac {9}{2} \\ y & = 3x + \dfrac {5}{2} \end{align}$
Persamaan garis singgung titik $\left(2, 9\right)$ adalah
$\begin{align} y - y_{2} & = m_{2} \left(x - x_{2}\right) \\ y - 9 & = 5 \left(x - 2\right) \\ y - 9 & = 5x - 10 \\ y & = 5x - 1 \end{align}$
Jadi, salah satu persamaan garis singgung tersebut sesuai pada opsi jawaban adalah $y = 5x - 1$
Jawab : B
Mencari Titik potong Grafik fungsi kurva dengan garis
$\begin{align} y_{\text{kurva}} & = y_{\text{garis}} \\ 2x^{2} − 3x + 7 & = 4x + 1 \\ 2x^{2} − 7x + 6 & = 0 \\ \left(2x-3\right)\left(x-2\right) & = 0 \end {align} \\ x_{1} = \dfrac {3}{2} \quad \text{atau} \quad x_{2} = 2 $
Selanjutnya, nilai absis $x_{1}$ dan $x_{1}$, kita substitusikan ke ke fungsi kurva atau garis untuk mendapatkan nilai ordinatnya. Agar lebih mudah kita pilih substitusikan ke fungsi garis saja.
$y = 4x + 1$
$x_{1} = \dfrac {3}{2} \; \Longrightarrow y = 4\left(\dfrac {3}{2}\right) + 1 = 7 \\ x_{2} = 2 \; \Longrightarrow y = 4\left(2\right) + 1 = 9$
Sehingga, diperoleh titik potong kurva dan garis tersebut adalah:
$\left(\frac {3}{2}, 7\right)$ dan $\left(2,9\right)$
Selanjutnya kita tentukan gradien garis singgung. Gradien merupakan turunan dari fungsi kurva $y = 2x^{2} − 3x + 7$
$m = y^{1} = \frac{dy}{dx} \\ m = 4x - 3$
Gradien garis singgung titik $\left(\frac {3}{2}, 7\right)$ adalah
$x_{1} = \dfrac {3}{2} \; \Longrightarrow m_{1} = 4\left(\dfrac {3}{2}\right) - 3 = 3$
Gradien garis singgung titik $\left(2, 9\right)$ adalah
$x_{2} = 2 \; \Longrightarrow m_{2} = 4\left(2\right) - 3 = 5$
Persamaan garis singgung titik $\left(\frac {3}{2}, 7\right)$ adalah
$\begin{align} y - y_{1} & = m_{1} \left(x - x_{1}\right) \\ y - 7 & = 3 \left(x - \dfrac {3}{2}\right) \\ y - 7 & = 3x - \dfrac {9}{2} \\ y & = 3x + \dfrac {5}{2} \end{align}$
Persamaan garis singgung titik $\left(2, 9\right)$ adalah
$\begin{align} y - y_{2} & = m_{2} \left(x - x_{2}\right) \\ y - 9 & = 5 \left(x - 2\right) \\ y - 9 & = 5x - 10 \\ y & = 5x - 1 \end{align}$
Jadi, salah satu persamaan garis singgung tersebut sesuai pada opsi jawaban adalah $y = 5x - 1$
Jawab : B
Soal Nomor 22
Sebuah akuarium tanpa tutup memiliki alas berbentuk persegi panjang dengan perbandingan panjang dan lebarnya 2 : 3. Jika luas permukaan akuarium adalah $1.800 \; \text{cm}^{2}$, volume maksimum akuarium tersebut adalah .........A. $\text {3.600 cm}^{3}$
B. $\text {5.400 cm}^{3}$
C. $\text {6.300 cm}^{3}$
D. $\text {7.200 cm}^{3}$
E. $\text {8.100 cm}^{3}$
Pembahasan Soal Nomor 22
BUKA
Penyelesaian :
Rumus Luas permukaan balok
Rumus Luas permukaan balok Tanpa Tutup
Diketahui :
$\begin{align} \text{L}_{p} & = 1.800 \; \text{cm}^{2} \\ \frac {p} {l} & = \frac{3}{2} \rightarrow p = \frac{3}{2}l \end{align}$
Mencari tinggi akuarium
$\begin{align} \text{L}_{p} & = pl + 2pt + 2lt \\ 1.800 & = \frac{3}{2}l.l + 2.\frac{3}{2}l.t. + 2lt \\ 1.800 & = \frac{3}{2}l^{2} + 3lt + 2lt \\ 1.800 & = \frac{3}{2}l^{2} + 5lt \\ 1.800 - \frac{3}{2}l^{2} & = 5lt \\ t & = \dfrac {1.800 - \frac{3}{2}l^{2}}{5l}\\ t & = \dfrac {360}{l} - \dfrac {3}{10}l \end {align}$
Mencari volume akuarium
$\begin {align} \text{V}\left(l\right) & = p \times l \times t \\ & = \frac{3}{2}l \times l \times \left(\dfrac {360}{l} - \dfrac {3}{10}l \right) \\ & = \frac{3}{2}l^{2}\times \left(\dfrac {360}{l} - \dfrac {3}{10}l \right) \\ & = 540l - \dfrac {9}{20}l^{3} \end {align}$
Volume akan maksimum bila turunan fungsi volume sama dengan nol
$\begin {align} V\left(l\right) & = 0 \\ 540l - \dfrac {9}{20}l^{3} & = 0 \\ 540 - \dfrac {27}{20}l^{2} & = 0 \\ 540 & = \dfrac {27}{20}l^{2} \\ l^{2} & = 540 \times \dfrac {20}{27} \\ l^{2} & = 400 \\ l & = 20 \end {align}$
Dengan demikian, volume akuarium akan maksimum bila lebarnya 20 cm
$\begin {align} V\left(l\right) & = 540l - \dfrac {9}{20}l^{3} \\ V\left(20\right) & = 540l - \dfrac {9}{20}l^{3} \\ & = 540 \left(20\right) - \dfrac {9}{20}.\left(20\right)^{3} \\ & = 10800 - \dfrac {9}{20}.8000 \\ & = 10800 - 3600 \\ & = \text {7.200 cm}^{3} \end {align}$
Jadi, volume maksimum akuarium tersebut adalah $\text {7.200 cm}^{3}$
Jawab : D
Rumus Luas permukaan balok
$\text{L}_{p} = 2\left(pl + pt + lt\right)$
Rumus Luas permukaan balok Tanpa Tutup
$\text{L}_{p} = pl + 2pt + 2lt$
Diketahui :
$\begin{align} \text{L}_{p} & = 1.800 \; \text{cm}^{2} \\ \frac {p} {l} & = \frac{3}{2} \rightarrow p = \frac{3}{2}l \end{align}$
Mencari tinggi akuarium
$\begin{align} \text{L}_{p} & = pl + 2pt + 2lt \\ 1.800 & = \frac{3}{2}l.l + 2.\frac{3}{2}l.t. + 2lt \\ 1.800 & = \frac{3}{2}l^{2} + 3lt + 2lt \\ 1.800 & = \frac{3}{2}l^{2} + 5lt \\ 1.800 - \frac{3}{2}l^{2} & = 5lt \\ t & = \dfrac {1.800 - \frac{3}{2}l^{2}}{5l}\\ t & = \dfrac {360}{l} - \dfrac {3}{10}l \end {align}$
Mencari volume akuarium
$\begin {align} \text{V}\left(l\right) & = p \times l \times t \\ & = \frac{3}{2}l \times l \times \left(\dfrac {360}{l} - \dfrac {3}{10}l \right) \\ & = \frac{3}{2}l^{2}\times \left(\dfrac {360}{l} - \dfrac {3}{10}l \right) \\ & = 540l - \dfrac {9}{20}l^{3} \end {align}$
Volume akan maksimum bila turunan fungsi volume sama dengan nol
$\begin {align} V\left(l\right) & = 0 \\ 540l - \dfrac {9}{20}l^{3} & = 0 \\ 540 - \dfrac {27}{20}l^{2} & = 0 \\ 540 & = \dfrac {27}{20}l^{2} \\ l^{2} & = 540 \times \dfrac {20}{27} \\ l^{2} & = 400 \\ l & = 20 \end {align}$
Dengan demikian, volume akuarium akan maksimum bila lebarnya 20 cm
$\begin {align} V\left(l\right) & = 540l - \dfrac {9}{20}l^{3} \\ V\left(20\right) & = 540l - \dfrac {9}{20}l^{3} \\ & = 540 \left(20\right) - \dfrac {9}{20}.\left(20\right)^{3} \\ & = 10800 - \dfrac {9}{20}.8000 \\ & = 10800 - 3600 \\ & = \text {7.200 cm}^{3} \end {align}$
Jadi, volume maksimum akuarium tersebut adalah $\text {7.200 cm}^{3}$
Jawab : D
Soal Nomor 23
Hasil dari $\displaystyle \int \dfrac {x^{2}}{\sqrt{x^{3}+2}}dx$ adalah .......A. $\dfrac {4}{3} \sqrt{x^{3}+2} + C $
B. $- \dfrac {4}{3} \sqrt{x^{3}+2} + C $
C. $\dfrac {2}{3} \sqrt{x^{3}+2} + C $
D. $- \dfrac {2}{3} \sqrt{x^{3}+2} + C $
E. $\sqrt{x^{3}+2} + C $
Pembahasan Soal Nomor 23
BUKA
Penyelesaian :
Untuk menyelesaikan soal integral di atas tidak bisa diselesaikan dengan cara biasa atau cara langsung dengan menggunakan rumus dasar integral . Sebab, Tipe soal integral di atas merupakan tipe soal integral subtitusi (soal integral yang diselesaikan dengan metode subtitusi).
Cara untuk membedakan tipe soal integral yang bisa diselesaikan dengan metode substitusi adalah Anda cukup menurunkan salah satu bagian (integran) dari soal tersebut. Jika turunannya ada hubungannya dengan bagian yang lain maka pakai integral substitusi. Namun, jika turunannya tidak ada hubungannya dengan bagian yang lain (biasanya ada x yang belum bisa diubah dalam u) maka pakai integral Parsial.
Langkah-langkah teknik pengintegralan metode substitusi :
Oke, langsung saja kita selesaikan soal integral di atas.
Misalkan :
$\begin {align} u & = x^{3} + 2 \\ \dfrac {du}{dx}& = 3x^{2} \\ 3x^{2} \; dx & = du \\ 3\left(x^{2}\right)\; dx & = du \\ x^{2}\; dx & = \dfrac{1}{3} du \\ \end {align}$
Permisalan di atas, kita subtitusikan kedalam soal
$\begin {align} & \quad \displaystyle \int \dfrac {x^{2}}{\sqrt{x^{3}+2}}dx \\ \\ & =\displaystyle \int \dfrac {\frac{1}{3} du}{\sqrt{u}} \\ \\ & = \displaystyle \int \dfrac{1}{3}.u^{-{1/2}}.du \\ \\ & = \dfrac {\frac{1}{3}}{-\frac{1}{2}+1} . u^{{1/2}} + C \\ \\ & = \dfrac {2}{3}. u^{{1/2}} + C \\ \\ & = \dfrac {2}{3}\left(x^{3} + 2\right)^{{1/2}} + C \\ \\ & = \dfrac {2}{3} \sqrt{x^{3}+2} + C \end {align}$
Jadi, hasil dari integral substitusi tersebut adalah $\dfrac {2}{3} \sqrt{x^{3}+2} + C$
Jawab : C
Untuk menyelesaikan soal integral di atas tidak bisa diselesaikan dengan cara biasa atau cara langsung dengan menggunakan rumus dasar integral . Sebab, Tipe soal integral di atas merupakan tipe soal integral subtitusi (soal integral yang diselesaikan dengan metode subtitusi).
Cara untuk membedakan tipe soal integral yang bisa diselesaikan dengan metode substitusi adalah Anda cukup menurunkan salah satu bagian (integran) dari soal tersebut. Jika turunannya ada hubungannya dengan bagian yang lain maka pakai integral substitusi. Namun, jika turunannya tidak ada hubungannya dengan bagian yang lain (biasanya ada x yang belum bisa diubah dalam u) maka pakai integral Parsial.
Langkah-langkah teknik pengintegralan metode substitusi :
- Misalkan salah satu fungsi sebagai u.
- Turunkan fungsi u terhadap x
- Bentuk hubungan keduanya (a dx = n du)
- Substitusi fungsi pemisalan ke bentuk integral awal
- Setelah diintegralkan, kembalikan fungsi pemisalan ke bentuk awalnya.
Oke, langsung saja kita selesaikan soal integral di atas.
Misalkan :
$\begin {align} u & = x^{3} + 2 \\ \dfrac {du}{dx}& = 3x^{2} \\ 3x^{2} \; dx & = du \\ 3\left(x^{2}\right)\; dx & = du \\ x^{2}\; dx & = \dfrac{1}{3} du \\ \end {align}$
Permisalan di atas, kita subtitusikan kedalam soal
$\begin {align} & \quad \displaystyle \int \dfrac {x^{2}}{\sqrt{x^{3}+2}}dx \\ \\ & =\displaystyle \int \dfrac {\frac{1}{3} du}{\sqrt{u}} \\ \\ & = \displaystyle \int \dfrac{1}{3}.u^{-{1/2}}.du \\ \\ & = \dfrac {\frac{1}{3}}{-\frac{1}{2}+1} . u^{{1/2}} + C \\ \\ & = \dfrac {2}{3}. u^{{1/2}} + C \\ \\ & = \dfrac {2}{3}\left(x^{3} + 2\right)^{{1/2}} + C \\ \\ & = \dfrac {2}{3} \sqrt{x^{3}+2} + C \end {align}$
Jadi, hasil dari integral substitusi tersebut adalah $\dfrac {2}{3} \sqrt{x^{3}+2} + C$
Jawab : C
Soal Nomor 24
Nilai $\displaystyle \int_{1}^{3} \left(6x^{2}-6x-6\right)dx$ adalah ........A. $16$
B. $20$
C. $22$
D. $32$
E. $38$
Pembahasan Soal Nomor 24
BUKA
Penyelesaian :
Rumus yang digunakan
$\begin{align} & \quad \displaystyle \int_{1}^{3} \left(6x^{2}-6x-6\right)dx \\ & = \left [2x^{3} - 3x^{2} - 6x \right]_{1}^{3} \\ & = \left [2 \left(3\right)^{3} - 3\left(3\right)^{2} - 6\left(3\right) \right] - \left [2 \left(1\right)^{3} - 3\left(1\right)^{2} - 6\left(1\right) \right] \\ & = \left(54 - 27 - 18\right) -\left(2 - 3 - 6\right) \\ & = 9 + 7 \\ & = 16 \end{align}$
Jadi, nilai dari integral tentu di atas adalah $16$
Jawab : A
Rumus yang digunakan
$\displaystyle \int_{a}^{b}f\left(x\right) dx = \left [F\left(x\right)\right]_{a}^{b} = F\left(b\right) - F\left(a\right)$
$\begin{align} & \quad \displaystyle \int_{1}^{3} \left(6x^{2}-6x-6\right)dx \\ & = \left [2x^{3} - 3x^{2} - 6x \right]_{1}^{3} \\ & = \left [2 \left(3\right)^{3} - 3\left(3\right)^{2} - 6\left(3\right) \right] - \left [2 \left(1\right)^{3} - 3\left(1\right)^{2} - 6\left(1\right) \right] \\ & = \left(54 - 27 - 18\right) -\left(2 - 3 - 6\right) \\ & = 9 + 7 \\ & = 16 \end{align}$
Jadi, nilai dari integral tentu di atas adalah $16$
Jawab : A
Soal Nomor 25
Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan jurusan tiga angka $080^{\circ}$ sejauh $\text{60 km}$. Kemudian berlayar menuju ke pelabuhan C dengan jurusan $200^{\circ}$ sejauh $\text{80 km}$. Jarak antara pelabuhan C dan A adalah ........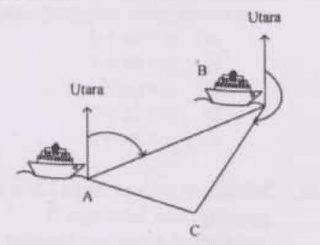
A. $10 \text{km}$
B. $5 \sqrt{13} \text{km}$
C. $10 \sqrt{13} \text{km}$
D. $20 \sqrt{13} \text{km}$
E. $100 \text{km}$
Pembahasan Soal Nomor 25
BUKA
Penyelesaian :
Perhatikan Rute perjalanan kapal berikut ini:

Berdasarkan gambar di atas, jarak A dan C adalah
Menggunakan Aturan Cosinus
$\begin{align} \text{AC}^{2} & = \text{AB}^{2} + \text{BC}^{2} - 2.\text{AB}.\text{BC}. \cos \beta \\ & = 60^{2} + 80^{2} - 2.60.80.\cos 60^{\circ} \\ & = 3600 + 6400 - 2.60.80.\dfrac {1}{2} \\ & = 10000 - 4800 \\ & = 5200 \\ \text{AC} & = \sqrt {5200} \\ & = \sqrt {400 \times 13} \\ & = 20 \sqrt {13} \end {align}$
Jadi, jarak antara pelabuhan C dan A adalah $20 \sqrt{13} \; \text{km}$
Jawab : D
Perhatikan Rute perjalanan kapal berikut ini:

Berdasarkan gambar di atas, jarak A dan C adalah
Menggunakan Aturan Cosinus
$\begin{align} \text{AC}^{2} & = \text{AB}^{2} + \text{BC}^{2} - 2.\text{AB}.\text{BC}. \cos \beta \\ & = 60^{2} + 80^{2} - 2.60.80.\cos 60^{\circ} \\ & = 3600 + 6400 - 2.60.80.\dfrac {1}{2} \\ & = 10000 - 4800 \\ & = 5200 \\ \text{AC} & = \sqrt {5200} \\ & = \sqrt {400 \times 13} \\ & = 20 \sqrt {13} \end {align}$
Jadi, jarak antara pelabuhan C dan A adalah $20 \sqrt{13} \; \text{km}$
Jawab : D
Soal Nomor 26
Himpunan penyelesaian persamaan $\cos2x − \sinx = 0,$ untuk $0 \leq x \leq 2\pi$ adalah .........A. $\dfrac {\pi}{6},\dfrac {5\pi}{6}, \pi $
B. $\dfrac {\pi}{6},\dfrac {5\pi}{6}, \dfrac {3\pi}{2} $
C. $\dfrac {\pi}{3},\dfrac {2\pi}{3}, \dfrac {3\pi}{2} $
D. $\dfrac {\pi}{3},\dfrac {4\pi}{3}, \dfrac {3\pi}{2} $
E. $\dfrac {7\pi}{6},\dfrac {3\pi}{2}, \dfrac {11\pi}{6} $
Pembahasan Soal Nomor 26
BUKA
Penyelesaian :
Untuk menyelesaikan soal persamaan trigonometri di atas, yang harus kita lakukan adalah mengubah bentuk soal persamaan trigonometrinya menjadi sejenis.
Dalam hal ini, kita mengubah cosinus $\left(\cos2x \right)$ menjadi sinus dengan menggunakan rumus trigonometri sudut ganda atau rangkap di bawah ini.
Rumus Trigonometri Sudut Ganda atau Rangkap
$ \cos 2\alpha = \cos^{2} \alpha - \sin^{2} \alpha \\ \cos 2\alpha = 2 \cos^{2} \alpha - 1 \\ \bbox[yellow,5px] {\cos 2\alpha = 1 - 2 \sin^{2} \alpha}$
Oke, mari kita selesaikan soal di atas.
$\begin{align} \cos2x − \sinx & = 0 \\ 1 - 2 \sin^{2} x - \sinx & = 0 \\ - 2 \sin^{2} x - \sinx + 1 & = 0 \\ 2 \sin^{2} x + \sinx - 1 & = 0 \\ \left(2 \sinx − 1\right) \left(\sin x + 1\right) & = 0 \\ \sin x = \dfrac {1}{2} \quad \text{atau} \quad \sin x & = -1 \end{align}$
Untuk $\sin x = \dfrac {1}{2}$ (positif), nilai $x$ nya berada pada kuadran I dan II.
$\begin {align} \sin x & = \dfrac {1}{2} \\ & = \sin 30^{\circ} \end {align}$
Kuadran I (satu)
$\begin {align} x & = 30^{\circ} \\ & = \dfrac {\pi}{6} \end {align}$
Kuadran II (dua)
$\begin {align} x & = 180^{\circ} - 30^{\circ} \\ & = 150^{\circ} \\ & = \dfrac {5\pi}{6} \end {align}$
Sedangkan untuk $\sin x = −1$ hanya mempunyai satu nilai pada interval $0 \leq x \leq 2\pi$.
$\begin {align} \sin x & = -1 \\ x & = 270^{\circ} \\ & = \dfrac {3\pi}{2} \end {align}$
Maka, himpunan penyelesaiannya adalah $\dfrac {\pi}{6},\dfrac {5\pi}{6}, \dfrac {3\pi}{2}$
Jawab : B
Untuk menyelesaikan soal persamaan trigonometri di atas, yang harus kita lakukan adalah mengubah bentuk soal persamaan trigonometrinya menjadi sejenis.
Dalam hal ini, kita mengubah cosinus $\left(\cos2x \right)$ menjadi sinus dengan menggunakan rumus trigonometri sudut ganda atau rangkap di bawah ini.
Rumus Trigonometri Sudut Ganda atau Rangkap
$ \cos 2\alpha = \cos^{2} \alpha - \sin^{2} \alpha \\ \cos 2\alpha = 2 \cos^{2} \alpha - 1 \\ \bbox[yellow,5px] {\cos 2\alpha = 1 - 2 \sin^{2} \alpha}$
Oke, mari kita selesaikan soal di atas.
$\begin{align} \cos2x − \sinx & = 0 \\ 1 - 2 \sin^{2} x - \sinx & = 0 \\ - 2 \sin^{2} x - \sinx + 1 & = 0 \\ 2 \sin^{2} x + \sinx - 1 & = 0 \\ \left(2 \sinx − 1\right) \left(\sin x + 1\right) & = 0 \\ \sin x = \dfrac {1}{2} \quad \text{atau} \quad \sin x & = -1 \end{align}$
Untuk $\sin x = \dfrac {1}{2}$ (positif), nilai $x$ nya berada pada kuadran I dan II.
$\begin {align} \sin x & = \dfrac {1}{2} \\ & = \sin 30^{\circ} \end {align}$
Kuadran I (satu)
$\begin {align} x & = 30^{\circ} \\ & = \dfrac {\pi}{6} \end {align}$
Kuadran II (dua)
$\begin {align} x & = 180^{\circ} - 30^{\circ} \\ & = 150^{\circ} \\ & = \dfrac {5\pi}{6} \end {align}$
Sedangkan untuk $\sin x = −1$ hanya mempunyai satu nilai pada interval $0 \leq x \leq 2\pi$.
$\begin {align} \sin x & = -1 \\ x & = 270^{\circ} \\ & = \dfrac {3\pi}{2} \end {align}$
Maka, himpunan penyelesaiannya adalah $\dfrac {\pi}{6},\dfrac {5\pi}{6}, \dfrac {3\pi}{2}$
Jawab : B
Soal Nomor 27
Diketahui $\sin\alpha\cos\beta = \dfrac{2}{5}$ dan $\left(\alpha + \beta \right) = \dfrac {5\pi}{6}.$ Nilai $\sin\left(\alpha − \beta\right) =.... $A. $- \dfrac {1}{2}$
B. $- \dfrac {3}{10}$
C. $- \dfrac {1}{10}$
D. $ \dfrac {3}{10}$
E. $ \dfrac {1}{2}$
Pembahasan Soal Nomor 27
BUKA
Penyelesaian :
Rumus Jumlah dan Selisih Dua Sudut Trigonometri :
Dik :
$\sin\alpha\cos\beta = \dfrac{2}{5} \\ \left(\alpha + \beta \right) = \dfrac {5\pi}{6} = \dfrac {5 \times 180^{\circ}}{6} = 150^{\circ}$
Perhatikan Rumus di atas !!!
Sebelum kita mencari nilai $\sin\left(\alpha − \beta\right)$, pertama-tama kita harus mencari nilai $\cos\alpha \sin\beta$ terlebih dahulu
.
Mencari Nilai $\cos\alpha \sin\beta$
Gunakan Rumus Jumlah Dua Sudut Trigonometri
$\begin{align} \sin \left(\alpha + \beta \right) & = \sin\alpha \cos\beta + \cos\alpha \sin\beta \\ \sin 150^{\circ} & = \sin\alpha \cos\beta + \cos\alpha \sin\beta \\ \dfrac{1}{2} & = \dfrac{2}{5} + \cos\alpha \sin\beta \\ \cos\alpha \sin\beta & = \dfrac{1}{2} - \dfrac{2}{5} \\ \cos\alpha \sin\beta & = \dfrac{1}{10} \end{align}$
Mencari Nilai $\sin\left(\alpha − \beta\right)$.
Substitusikan nilai $\sin\alpha \cos\beta$ dan $\cos\alpha \sin\beta$ kedalam rumus selisih dua sudut triogonometri di atas.
$\begin{align} \sin \left(\alpha - \beta \right) & = \sin\alpha \cos\beta - \cos\alpha \sin\beta \\ & = \dfrac{2}{5} - \dfrac{1}{10} \\ & = \dfrac{3}{10} \end{align}$
Jadi, nilai $\sin\left(\alpha − \beta\right)$ adalah $\dfrac{3}{10} $
Jawab : D
Rumus Jumlah dan Selisih Dua Sudut Trigonometri :
$\sin \left(\alpha + \beta \right) = \sin\alpha\cos\beta + \cos\alpha \sin\beta$
$\sin \left(\alpha - \beta \right) = \sin\alpha\cos\beta - \cos\alpha \sin\beta$
$\sin \left(\alpha - \beta \right) = \sin\alpha\cos\beta - \cos\alpha \sin\beta$
Dik :
$\sin\alpha\cos\beta = \dfrac{2}{5} \\ \left(\alpha + \beta \right) = \dfrac {5\pi}{6} = \dfrac {5 \times 180^{\circ}}{6} = 150^{\circ}$
Perhatikan Rumus di atas !!!
Sebelum kita mencari nilai $\sin\left(\alpha − \beta\right)$, pertama-tama kita harus mencari nilai $\cos\alpha \sin\beta$ terlebih dahulu
.
Mencari Nilai $\cos\alpha \sin\beta$
Gunakan Rumus Jumlah Dua Sudut Trigonometri
$\begin{align} \sin \left(\alpha + \beta \right) & = \sin\alpha \cos\beta + \cos\alpha \sin\beta \\ \sin 150^{\circ} & = \sin\alpha \cos\beta + \cos\alpha \sin\beta \\ \dfrac{1}{2} & = \dfrac{2}{5} + \cos\alpha \sin\beta \\ \cos\alpha \sin\beta & = \dfrac{1}{2} - \dfrac{2}{5} \\ \cos\alpha \sin\beta & = \dfrac{1}{10} \end{align}$
Mencari Nilai $\sin\left(\alpha − \beta\right)$.
Substitusikan nilai $\sin\alpha \cos\beta$ dan $\cos\alpha \sin\beta$ kedalam rumus selisih dua sudut triogonometri di atas.
$\begin{align} \sin \left(\alpha - \beta \right) & = \sin\alpha \cos\beta - \cos\alpha \sin\beta \\ & = \dfrac{2}{5} - \dfrac{1}{10} \\ & = \dfrac{3}{10} \end{align}$
Jadi, nilai $\sin\left(\alpha − \beta\right)$ adalah $\dfrac{3}{10} $
Jawab : D
Soal Nomor 28
Nilai dari $\dfrac {\sin280^{\circ} - \sin140^{\circ}}{\cos280^{\circ} - \cos140^{\circ}} = ....$ A. $- \sqrt{3}$
B. $- \sqrt{2}$
C. $- \dfrac{1}{2} \sqrt{3}$
D. $ \sqrt{2}$
E. $ \sqrt{3}$
Pembahasan Soal Nomor 28
BUKA
Penyelesaian :
Rumus Selisih pada Sinus dan Cosinus
Oke, mari kita selesaikan soal di atas.
$\begin{align} & \quad \dfrac {\sin280^{\circ} - \sin140^{\circ}}{\cos280^{\circ} - \cos140^{\circ}} \\ \\ & = \dfrac {2 \cos \dfrac{1}{2} \left(280^{\circ}+140^{\circ} \right) \; \sin\dfrac{1}{2} \left(280^{\circ}-140^{\circ} \right)}{-2 \sin \dfrac{1}{2} \left(280^{\circ}+140^{\circ} \right) \; \sin\dfrac{1}{2} \left(280^{\circ}-140^{\circ} \right)}\\ \\ & = \dfrac {2 \cos 210^{\circ} \sin 70^{\circ}}{-2 \sin 210^{\circ} \sin 70^{\circ}} \\ \\ & = - \dfrac {\cos 210^{\circ}}{\sin 210^{\circ}} \\ \\ & = - \dfrac {\cos \left(180^{\circ}+30^{\circ}\right)}{\sin \left(180^{\circ}+30^{\circ}\right)} \\ \\ & = - \dfrac {- \cos 30^{\circ}}{- \sin 30^{\circ}} \\ \\ & = - \dfrac {- \dfrac{1}{2} \sqrt{3} }{- \dfrac{1}{2}} \\ \\ & = - \sqrt{3} \end{align}$
Jadi, nilai dari $\dfrac {\sin280^{\circ} - \sin140^{\circ}}{\cos280^{\circ} - \cos140^{\circ}}$ adalah $- \sqrt{3}$
Jawab : A
Rumus Selisih pada Sinus dan Cosinus
$\sin A - \sin B = 2 \cos \dfrac{1}{2} \left(A+B\right) \; \sin\dfrac{1}{2} \left(A-B\right)$
$\cos A - \cos B = -2 \sin \dfrac{1}{2} \left(A+B\right) \; \sin\dfrac{1}{2} \left(A-B\right)$
$\cos A - \cos B = -2 \sin \dfrac{1}{2} \left(A+B\right) \; \sin\dfrac{1}{2} \left(A-B\right)$
Oke, mari kita selesaikan soal di atas.
$\begin{align} & \quad \dfrac {\sin280^{\circ} - \sin140^{\circ}}{\cos280^{\circ} - \cos140^{\circ}} \\ \\ & = \dfrac {2 \cos \dfrac{1}{2} \left(280^{\circ}+140^{\circ} \right) \; \sin\dfrac{1}{2} \left(280^{\circ}-140^{\circ} \right)}{-2 \sin \dfrac{1}{2} \left(280^{\circ}+140^{\circ} \right) \; \sin\dfrac{1}{2} \left(280^{\circ}-140^{\circ} \right)}\\ \\ & = \dfrac {2 \cos 210^{\circ} \sin 70^{\circ}}{-2 \sin 210^{\circ} \sin 70^{\circ}} \\ \\ & = - \dfrac {\cos 210^{\circ}}{\sin 210^{\circ}} \\ \\ & = - \dfrac {\cos \left(180^{\circ}+30^{\circ}\right)}{\sin \left(180^{\circ}+30^{\circ}\right)} \\ \\ & = - \dfrac {- \cos 30^{\circ}}{- \sin 30^{\circ}} \\ \\ & = - \dfrac {- \dfrac{1}{2} \sqrt{3} }{- \dfrac{1}{2}} \\ \\ & = - \sqrt{3} \end{align}$
Jadi, nilai dari $\dfrac {\sin280^{\circ} - \sin140^{\circ}}{\cos280^{\circ} - \cos140^{\circ}}$ adalah $- \sqrt{3}$
Jawab : A
Soal Nomor 29
Diketahui kubus ABCD.EFGH dengan panjang rusuknya $\text{6 cm}.$ Jika $\alpha$ adalah sudut antara bidang AFH dan bidang BDHF, nilai $\sin\alpha = .....$A. $\dfrac{1}{2}$
B. $\dfrac{1}{3} \sqrt{3}$
C. $\dfrac{1}{2} \sqrt{2}$
D. $\dfrac{1}{2} \sqrt{3}$
E. $\dfrac{2}{3} \sqrt{2}$
Pembahasan Soal Nomor 29
BUKA
Penyelesaian :
Perhatikan gambar ilustrasinya di bawah ini :
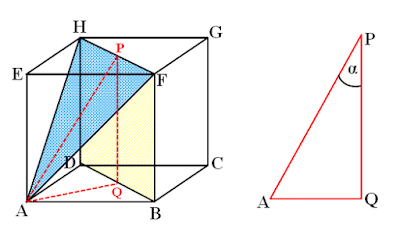
Berdasarkan gambar di atas maka diperoleh :
Panjang PQ sama dengan panjang sisi kubus sedangkan panjang AQ sama dengan panjang setengah diagonal bidang. Sehingga:
$\begin{align} PQ & = \text{6 cm} \\ AQ & = \dfrac {1}{2} \times \text {diagonal bidang} \\ AQ & = \dfrac {1}{2} \times 6\sqrt{2} \\ AQ & = 3\sqrt{2} \; \text{cm} \end{align}$
Mencari Panjang AP
$\begin{align} AP & = \sqrt{PQ^{2} + AQ^{2}} \\ & = \sqrt{6^{2} + \left(3\sqrt{2}\right)^{2}} \\ & = \sqrt{36 + 18} \\ & = \sqrt{54} \\ & = \sqrt{9 \times 6} \\ & = 3\sqrt{6} \end{align}$
Maka, nilai $\sin\alpha$ adalah
$\begin{align} \sin\alpha & = \dfrac {AQ}{AP} \\ & = \dfrac {3\sqrt{2}}{3\sqrt{6}} \\ & = \dfrac {\sqrt{1}}{\sqrt{3}} \\ & = \dfrac {1}{3} \sqrt{3} \end{align}$
Jadi, nilai sinus sudut antara bidang AFH dan bidang BDHF adalah $\dfrac {1}{3} \sqrt{3}$
Jawab : D
Perhatikan gambar ilustrasinya di bawah ini :

Berdasarkan gambar di atas maka diperoleh :
Panjang PQ sama dengan panjang sisi kubus sedangkan panjang AQ sama dengan panjang setengah diagonal bidang. Sehingga:
$\begin{align} PQ & = \text{6 cm} \\ AQ & = \dfrac {1}{2} \times \text {diagonal bidang} \\ AQ & = \dfrac {1}{2} \times 6\sqrt{2} \\ AQ & = 3\sqrt{2} \; \text{cm} \end{align}$
Mencari Panjang AP
$\begin{align} AP & = \sqrt{PQ^{2} + AQ^{2}} \\ & = \sqrt{6^{2} + \left(3\sqrt{2}\right)^{2}} \\ & = \sqrt{36 + 18} \\ & = \sqrt{54} \\ & = \sqrt{9 \times 6} \\ & = 3\sqrt{6} \end{align}$
Maka, nilai $\sin\alpha$ adalah
$\begin{align} \sin\alpha & = \dfrac {AQ}{AP} \\ & = \dfrac {3\sqrt{2}}{3\sqrt{6}} \\ & = \dfrac {\sqrt{1}}{\sqrt{3}} \\ & = \dfrac {1}{3} \sqrt{3} \end{align}$
Jadi, nilai sinus sudut antara bidang AFH dan bidang BDHF adalah $\dfrac {1}{3} \sqrt{3}$
Jawab : D
Soal Nomor 30
Diketahui kubus KLMN.OPQR dengan panjang rusuk 6 cm. Jarak titik M ke bidang LNQ adalah ........A. $2 \sqrt {2} \; \text{cm}$
B. $2 \sqrt {3} \; \text{cm}$
C. $3 \sqrt {2} \; \text{cm}$
D. $2 \sqrt {3} \; \text{cm}$
E. $4 \sqrt {3} \; \text{cm}$
Pembahasan Soal Nomor 30
BUKA
Penyelesaian :
Perhatikan gambar ilustrasi dibawah ini :
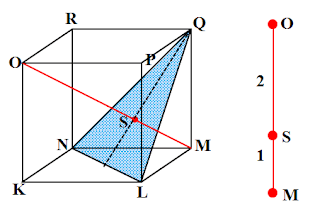
Jarak titik M ke bidang LNQ adalah garis MS. Ternyata bila garis MS diperpanjang akan tepat melalui titik O, di mana MO adalah diagonal ruang.
$\begin{align} MO & = a \sqrt{3} \\ & = 6\sqrt{3} \; \text{cm} \end{align}$
Perbandingan antara $MS : SO = 1 : 2$, sehingga:
$\begin{align} MS & = \dfrac {1}{3} \times \text{diagonal ruang} \\ & = \dfrac {1}{3} \times MO \\ & = \dfrac {1}{3} \times 6\sqrt{3} \\ & = 2\sqrt{3} \end{align}$
Jadi, jarak titik M ke bidang LNQ adalah $2 \sqrt {3} \; \text{cm}$
Jawab : B
Perhatikan gambar ilustrasi dibawah ini :

Jarak titik M ke bidang LNQ adalah garis MS. Ternyata bila garis MS diperpanjang akan tepat melalui titik O, di mana MO adalah diagonal ruang.
$\begin{align} MO & = a \sqrt{3} \\ & = 6\sqrt{3} \; \text{cm} \end{align}$
Perbandingan antara $MS : SO = 1 : 2$, sehingga:
$\begin{align} MS & = \dfrac {1}{3} \times \text{diagonal ruang} \\ & = \dfrac {1}{3} \times MO \\ & = \dfrac {1}{3} \times 6\sqrt{3} \\ & = 2\sqrt{3} \end{align}$
Jadi, jarak titik M ke bidang LNQ adalah $2 \sqrt {3} \; \text{cm}$
Jawab : B
Demikianlah pembahasan soal UN Matematika SMA IPA 2017 part.3 No. 21 - 30 dan jangan lupa kunjungi artikel menarik lainnya di blog ini.
NEXT :
Pembahasan Soal UN Matematika SMA IPA 2017 Part.4 No. 31 - 40
Terima kasih telah berkunjung dan meluangkan waktunya untuk membaca artikel sederhana ini yang berjudul "Pembahasan Soal UN Matematika SMA No. 21 - 30". Semoga informasi yang terkandung dalam tulisan ini dapat bermanfaat bagi anda yang membutuhkannya.
Salam sukses untuk kita semua....!!!
Note : Silahkan dikoreksi dan berikan komentar jika ada kesalahan atau masih ada keambiguan baik dalam soal maupun penyelesaian soal ini.